Moon phase and position with Pyorbital¶
It is possible to calculate the phase and position of the moon at any given time in the past or future. This is done by an implementation of the astronimical methods described at Stjaernhimlen. The calculations have been compared to the pyephem library, and deviations are small, see below.
Computing the phase of the moon¶
>>> from datetime import datetime
>>> from pyorbital.moon_phase import moon_phase
>>> time_t = datetime(2011, 12, 1, 12)
>>> print moon_phase(time_t)
0.409752921579
It works also with datetime sequences:
>>> import numpy as np
>>> from pyorbital.moon_phase import moon_phase
>>> time_t = np.arange('2005-02', '2005-03', dtype='datetime64[D]')
>>> print moon_phase(time_t)
[ 6.36537786e-01 5.32201222e-01 4.23413367e-01 3.15141455e-01
2.13350898e-01 1.24769455e-01 5.62102473e-02 1.34598103e-02
4.68042562e-05 1.64235364e-02 5.99725484e-02 1.25824054e-01
2.08064456e-01 3.00824090e-01 3.98939205e-01 4.98161316e-01
5.95059508e-01 6.86787971e-01 7.70852355e-01 8.44942289e-01
9.06852663e-01 9.54487201e-01 9.85925226e-01 9.99530703e-01
9.94086558e-01 9.68941138e-01 9.24152715e-01 8.60612554e-01]
Computing the position of the moon¶
>>> from datetime import datetime
>>> from pyorbital import planets
>>> time_t = datetime(2016, 7, 30, 0, 0)
>>> moon = planets.Moon(time_t)
>>> lon = 20.0
>>> lat = 65.0
>>> rasc, decl, alt, azi = moon.topocentric_position(lon, lat)
>>> print alt, azi
6.33389454706 61.6795817556
And for an array of longitudes and latitudes:
>>> import numpy as np
>>> lons = np.arange(100).reshape(10,10)
>>> lats = np.arange(100).reshape(10,10) * 0.9
>>> rasc, decl, alt, azi = moon.topocentric_position(lons, lats)
>>> print alt.shape
(10, 10)
>>> print alt[4,8]
14.9564426346
Accuracy¶
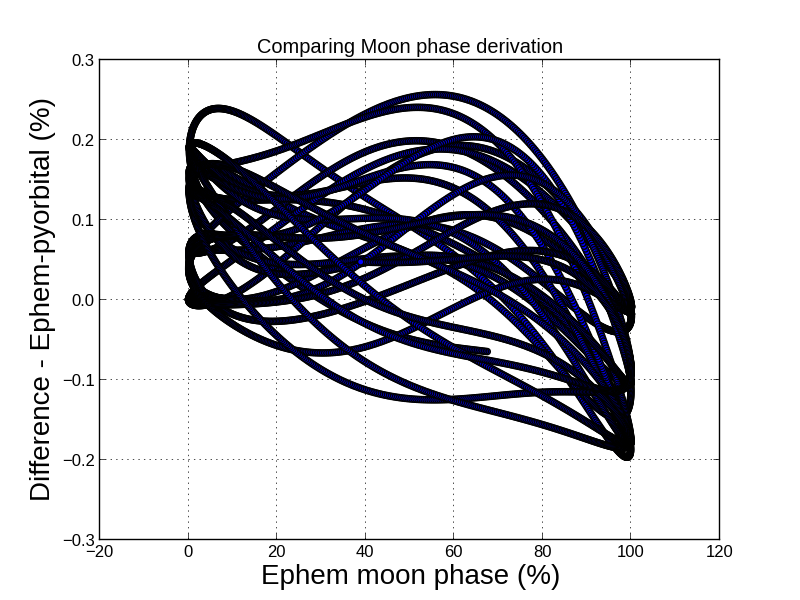
In lack of an absolute truth or reference the moon calclations with Pyorbital have been compared to pyephem. There are indeed deviations, but for the moon phase they are in general rather small. See image below, where we compare the moon phase over 416 days starting from December 1st 2015. As seen from the figure the deviations are within 0.3 %.
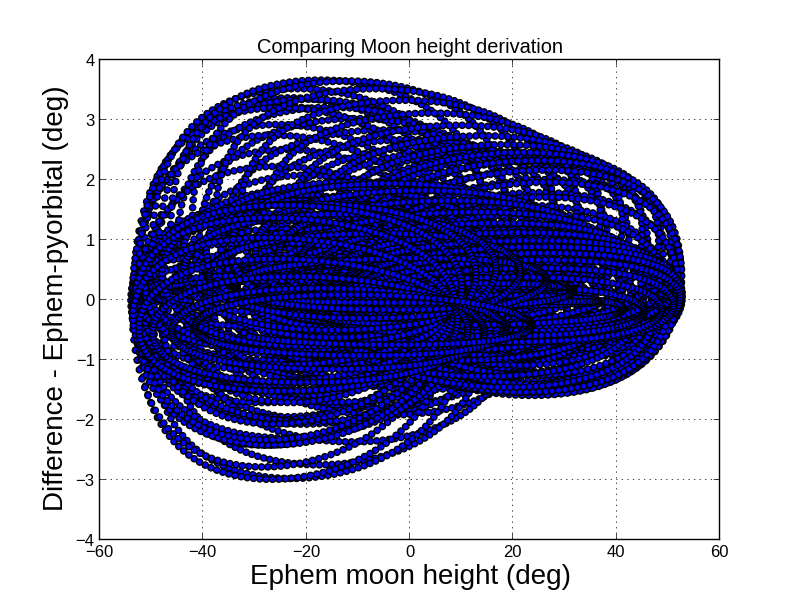
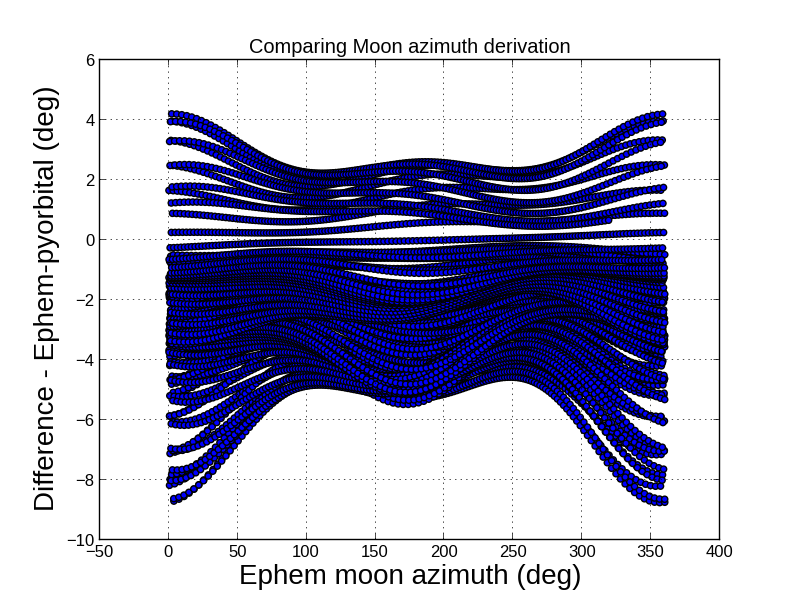
For moon height and azimuth differences are larger, as seen from the figures below. We have calculated the position of the moon relative to the City of Norrköping, Sweden, over four months from March 7, 2012. The deviations are within 4 degrees for the height, and within 9 degrees for the azimuth.